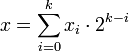Záporná čísla ve dvojkové soustavě
Potřeba zpracovávání záporných čísel přinesla nutnost doplnit kódování čísla v binární soustavě o formát nebo příznak záporné hodnoty.
Přímý kód
Přímý kód je jednoduchým způsobem vyjádření záporného čísla tak, že je nejvyšší bit vyhrazen znaménku. Tento jednoduchý způsob je však vyvážen nevýhodou
komplikovaného algoritmu zpracování čísel a navíc, tento způsob vytváří dvě možné reprezentace čísla 0 (nula). Kladné číslo je na nejvyšším bitu
indikováno stavem 0, stavem 1 pak záporné číslo.
| přímý kód |
| bit |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
| znaménko/váha bitu |
S |
26 |
25 |
24 |
23 |
22 |
21 |
20 |
| záporné přímé binární číslo |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
dekadicky: -21 |
| kladné přímé binární číslo |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
dekadicky: 21 |
Inverzní kód
Inverzní kód vyjadřuje záporná čísla jako prostou binární negaci všech bitů. Nevýhody kódu jsou stejné jako u přímého kódu.
| inverzní kód |
| bit |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
| znaménko/váha bitu |
S |
26 |
25 |
24 |
23 |
22 |
21 |
20 |
| záporné inverzní binární číslo |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
dekadicky: -106 |
| kladné inverzní binární číslo |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
dekadicky: 106 |
Aditivní kód
Aditivní kód, též kód s posunutou nulou, nemá přímo vyhrazený bit pro znaménko a pracuje na principu posunutí nuly, tedy k binárně kódované hodnotě je při dekódování
přičítána známá hodnota odpovídající polovině možných kombinací vyjádřených na daném počtu bitů, například na 8 bitech je tato hodnota 128, při tomto
kódování nejvyšší bit vyjadřuje kladné číslo stavem 1 na nejvyšším bitu, stavem 0 pak záporné číslo, odstraňuje možnost dvojitého zobrazování nuly
jako kladné i záporné.
V příkladu je uveden postup dekódování binárně zapsaného celého čísla pomocí aditivního kódu, kódování se provádí opačným postupem.
| aditivní kód |
| bit |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
| znaménko/váha bitu |
27 |
26 |
25 |
24 |
23 |
22 |
21 |
20 |
| kladné aditivní binární číslo |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
dekadicky: 149 - 128 = 21 |
| záporné aditivní binární číslo |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
dekadicky: 21 - 128 = -107 |
| Poznámka |
| Ačkoliv se aditivní kód nepoužívá pro zpracování celých čísel, našel uplatnění při reprezentaci reálných čísel; exponentu. |
Dvojkový doplněk
Dvojkový doplněk je kombinací vyjádření čísla pomocí inverzního a aditivního kódu. Jeho princip umožňuje snadné zpracování v matematických jednotkách
výpočetní techniky, odstraňuje možnost dvojitého zobrazování nuly jako kladné i záporné.
V příkladu je uveden postup dekódování binárně zapsaného celého čísla pomocí dvojkového doplňku, kódování se provádí opačným postupem.
| dvojkový doplněk |
| bit |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
| znaménko/váha bitu |
S |
26 |
25 |
24 |
23 |
22 |
21 |
20 |
| kladné binární číslo |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
dekadicky: 21 |
| záporné binární číslo |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
|
| odečtení 1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
|
| negace |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
dekadicky: -107 |
|
znaménko "-" přechází k absolutní hodnotě jako obsah nejvyššího bitu "S" = 1 |
|