PLC - Programovatelné logické automaty
PLC-AUTOMATIZACE - DATA - KÓDOVÁNÍ / DEKÓDOVÁNÍ - BINÁRNÍ Provoz webu zajišťuje:

www.hapesoft.cz

BINÁRNÍ KÓDOVÁNÍ

Charakteristika

Binární kódování představuje reprezentaci informace v soustavě zápisu, kdy se k zápisu používá pouze dvou primitivních znaků, které vyjadřující hodnoty ano/ne, je/není eventuelně, v elektrotechnice, zapnuto/vypnuto. Pomocí binárního kódu je možno přiřadit dané informaci množinu (skupinu) binárních (dvojkových) signálů (stavů). Množina binárních signálů musí mít takovou minimální velikost, aby v ní bylo možno vyjádřit všechny kombinace potřebné pro vyjádření informace. V případě potřeby je možno množiny řetězit, sdružovat.

Pro kódování je nutno znát pravidlo jakým se informace převede do binárního kódu (šifrování) a analogicky reverzní pravidlo pro dekódování informace (dešifrování). Binární kódování neobsahuje informaci o algoritmu, jakým bylo vytvořeno.

Ve výpočetní technice je signál reprezentován Bitem a množiny jsou reprezentovány jako Nibble, Byte, Word, DWord, QWord.

Historie

Binární systém, který se stal základem moderního binárního systému vytvořil Gottfried Wilhelm Leibniz v roce 1679 a publikoval jej v článku Explication de l'Arithmétique Binaire tj. vysvětlení binární aritmetiky, kdy jsou používány pouze hodnoty 0 a 1. Při své práci narazil i na čínské dokumenty pracující s binárním kódem učence Fu Xi a text I Ching (9. století př.n.l.) Porovnáním těchto zdrojů se svými výsledky jej přesvědčilo o správnosti a aplikovatelnosti jeho závěrů zvláště, když nalezl binární hexagram.

Binární systém není pouze doménou materiálního vyjádření něčeho co je nebo není ale principielně jej používaly a používají i Africké a Asijské kmeny pro předávání zpráv akustickým způsobem pomocí bubnů (Slit drum).

Ve francouzské Polynésii, na ostrově Mangareva, byl používán hybridní binárně desítkový systém již před rokem 1450.

Učenec a filozof Shao Yong vyvinul v 11. století metodu pro uspořádání hexagramu s takovou precizností, že se později ukázalo, že odpovídá, kódové sekvenci 0-63. Hexagram používá takové seskupení množin, kdy jednotlivé dílčí části jsou nebo nejsou spojeny, tedy vyjadřují stav 1 nebo 0 a nejméně významná informace je uložena na obvodu. Výsledná kombinace je pak složena ze dvou prvků množiny (8 x 8).

V roce 1605, Francis Bacon vytvořil systém, který prováděl náhradu písmen abecedy sekvencí binárních číslic tak, aby se tento kód vložený do libovolného textu stal skrytým.

Další matematik a filozof, George Boole, vydal v roce 1847 pojednání pod názvem názvem The Mathematical Analysis of Logic "Matematická analýza logiky", které popisuje algebraický systém logiky. V současnosti známý jako Booleova algebra. Systém Booleov algebry je založena na binárních stavech, tedy ano-ne a obsahuje tři základnější operace: AND, OR a NOT. Později si student Claude Shannon povšiml, že Booleova algebra se nápadně podobá elektrickém obvodu a v roce 1937 sepsal na toto téma svoji práci, která se stala východiskem pro využití binárního kódu v praktických aplikacích, jako jsou počítače, elektrické obvody.

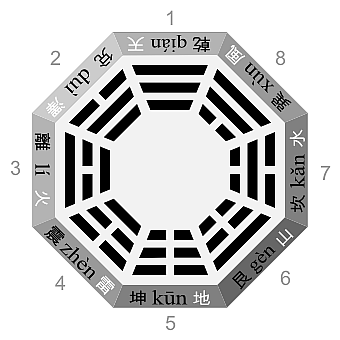hexagram Ba Gua
Obrázek 1
Hexagram Ba Gua.

Mezi binární kódy patří i Braillovo písmo a Morseova abeceda.

Příklady binárních kódů

4 bity

5 bitů

  • Systémy s vlastním kódem
    • J. Lyons and Co. LEO (Lyon's Electronic Office)
    • English Electric DEUCE
    • University of Illinois at Urbana-Champaign ILLIAC
    • ZEBRA
    • EMI 1100
    • Ferranti Mercury, Pegasus, a Orion systémy
  • Standardní kódy
    • International Telegraph Alphabet No 1 (ITA1) - Mezinárodní telegrafní abeceda 1 - Baudot kód
    • International Telegraph Alphabet No 2 (ITA2) - Mezinárodní telegrafní abeceda 2 - Murray kódu
    • American Teletypewriter code (USTTY) - Americký dálnopisný kód - varianta ITA2 používaná v USA
    • DIN 66006 - vyvinutý pro prezentaci ALGOL - Alcor programy na děrné pásky a děrné štítky
    • Stegonografický kód - též Baconova šifra

6 bitů

  • International Telegraph Alphabet No 3 (ITA3) - odvozený z kódu Moore ARQ, taktéž označovaný jako RCA
  • BCD (Binary Coded Decimal) - pro sálové počítače
  • ASCII - podmnožina kódování 7 bitů ASCII
  • Braille - Braillovo slepecké písmo, znaky jsou reprezentovány šesticí bodů

7 bitů

  • ASCII - rozšířený ASCII kód, definován jako sedm-bitové znakové sady
  • CCIR 476 - rozšiřuje ITA2 na 7 bitů, kontrolní čislice
  • International Telegraph Alphabet No 4 (ITA4)

8 bitů

  • Rozšířený kód ASCII - různé normy rozšíření ASCII na osmi bitů, o dalších 128 znaků
    • ISO / IEC 8859
    • Mac OS Roman
    • Windows-1252
  • EBCDIC - používaný u prvních IBM počítačů ale i u současného SYSTEM IBM
  • BCD (Binary Coded Decimal) - komprimovaný (2 znaky) / nekomprimovaný (1 znak)

10 bitů

  • Autospec - Bauerův kód. Autospec opakuje 5ti bitový znak dvakrát, ale v případě, že se jedná o lichou paritu, je opakovaný znak převrácený

16 bitů

  • UCS-2 - dřívější kódování schopné reprezentovat základní vícejazyčné sady Unicode / pro jeden znak jsou rezervovány 2 Byte

32 bitů

  • UTF-32 / UCS-4 - novější reprezentace kódování vícejazyčných sad Uicode / pro jeden znak jsou rezervovány 4 Byte

Variabilní počet bitů

  • Dvojková číselná soustava - zobrazování čísel v binární formě
  • UTF-8 - kódování znaků s využitím převládajícího souladu s ASCII, ale může reprezentovat i úplné Unicode se sekvencemi 4-8 bitů
  • UTF-16 - rozšiřuje UCS-2 na celé Unicode se sekvencí 1 nebo 2 16-bitových prvků
  • CZ 18.030 - úplný Unicode kód s proměnnou délkou je určen pro zajištění kompatibility se starším čínským multibyteovým kódováním
  • Huffmanovo kódování - technika pro vyjádření více společných znaků s použitím kratších řetězců pro často se opakující sekvence znaků
  • Morseova abeceda
PLC-AUTOMATIZACE - DATA - KÓDOVÁNÍ / DEKÓDOVÁNÍ - BINÁRNÍ
Reference:

Historie

  • Bacon, Francis (1605). "The Advancement of Learning" 6. London. Chapter 1.
  • Bender, Andrea; Beller, Sieghard (16 December 2013). "Mangarevan invention of binary steps for easier calculation". Proceedings of the National Academy of Sciences.
  • Aiton, Eric J. (1985). Leibniz: A Biography. Taylor & Francis. pp. 245–8. ISBN 0-85274-470-6.
  • J.E.H. Smith (2008). Leibniz: What Kind of Rationalist?: What Kind of Rationalist?. Springer. p. 415. ISBN 978-1-4020-8668-7.
  • Yuen-Ting Lai (1998). Leibniz, Mysticism and Religion. Springer. pp. 149–150. ISBN 978-0-7923-5223-5.
  • W. S. Anglin and J. Lambek, The Heritage of Thales, Springer, 1995, ISBN 0-387-94544-X
  • Wilhelm, Richard (1950). The I Ching or Book of Changes. trans. by Cary F. Baynes, forward by C. G. Jung, preface to 3rd ed. by Hellmut Wilhelm (1967). Princeton, NJ: Princeton University Press. pp. 266, 269. ISBN 0-691-09750-X.Edward Hacker; Steve Moore; Lorraine Patsco (2002). I Ching: An Annotated Bibliography. Routledge. p. 13. ISBN 978-0-415-93969-0.
  • Jonathan Shectman (2003). Groundbreaking Scientific Experiments, Inventions, and Discoveries of the 18th Century. Greenwood Publishing. p. 29. ISBN 978-0-313-32015-6.
  • Sanchez, Julio; Canton, Maria P. (2007). Microcontroller programming: the microchip PIC. Boca Raton, Florida: CRC Press. p. 37. ISBN 0-8493-7189-9.
  • Ryan, James A. (January 1996). "Leibniz' Binary System and Shao Yong's "Yijing"". Philosophy East and West (University of Hawaii Press) 46 (1): 59–90. doi:10.2307/1399337. JSTOR 1399337.
  • Leibniz G., Explication de l'Arithmétique Binaire, Die Mathematische Schriften, ed. C. Gerhardt, Berlin 1879
 
 
Publikovaný obsah je určen pouze pro individuální studium.
Není povolena distribuce, prodej, přetisk a použití textu a/nebo vyobrazení (úplný, dílčí a/nebo částečný), použití ke školení a/nebo výuce (hromadné, skupinové nebo zadávané), veřejné a/nebo skupinové prezentace a ani jiné formy šíření v hmotné a/nebo nehmotné podobě.